Maclaurin's inequality
In mathematics, Maclaurin's inequality, named after Colin Maclaurin, is a refinement of the inequality of arithmetic and geometric means.
Let a1, a2, ..., an be positive real numbers, and for k = 1, 2, ..., n define the averages Sk as follows:
The numerator of this fraction is the elementary symmetric polynomial of degree k in the n variables a1, a2, ..., an, that is, the sum of all products of k of the numbers a1, a2, ..., an with the indices in increasing order. The denominator is the number of terms in the numerator, the binomial coefficient 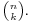
Maclaurin's inequality is the following chain of inequalities:
with equality if and only if all the ai are equal.
For n = 2, this gives the usual inequality of arithmetic and geometric means of two numbers. Maclaurin's inequality is well illustrated by the case n = 4:
Maclaurin's inequality can be proved using the Newton's inequalities.
See also
References
- Biler, Piotr; Witkowski, Alfred (1990). Problems in mathematical analysis. New York, N.Y.: M. Dekker. ISBN 0824783123.
This article incorporates material from MacLaurin's Inequality on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
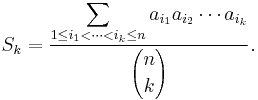
![S_1 \geq \sqrt{S_2} \geq \sqrt[3]{S_3} \geq \cdots \geq \sqrt[n]{S_n}](/2012-wikipedia_en_all_nopic_01_2012/I/ffe8b7a45d0608396daf07402fe919df.png)
![\begin{align}
& {} \quad \frac{a_1%2Ba_2%2Ba_3%2Ba_4}{4} \\[8pt]
& {} \ge \sqrt{\frac{a_1a_2%2Ba_1a_3%2Ba_1a_4%2Ba_2a_3%2Ba_2a_4%2Ba_3a_4}{6}} \\[8pt]
& {} \ge \sqrt[3]{\frac{a_1a_2a_3%2Ba_1a_2a_4%2Ba_1a_3a_4%2Ba_2a_3a_4}{4}} \\[8pt]
& {} \ge \sqrt[4]{a_1a_2a_3a_4}.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/6d34451f322046cf5f074dcb32d0602e.png)